Ancient Greek Philosophy Part 4 - Parmenides and Zeno of Elea
Parmenides of Elea (~515 BC - unknown BC) was the founder of the Greek school of Eleaticism. He reportedly only wrote one work, entitled On Nature, of which only fragments remain. The largest contribution that Parmenides made to philosophy was of Monism. Monism is the metaphysical assertion that all is one. This statement seems to be both true and contradictory at the same time, depending on how you look at it. This idea is also consistent with the quintessential substance concept that I talked about with Thales. Monism as an idea is also a precursor to the much later pantheist ideas of Baruch Spinoza, only without the religious implications.
More remains of the writings and ideas of Parmenides student, Zeno. Zeno's is remembered for his list of supposed paradoxes. Originally numbering around 40, only 10 are known about, as they are discussed by later Greek philosophers. Most of them are not so much paradoxes as they are misunderstandings about the relationship between human language and the nature of reality, framed in a way which makes reality seen absurd. Zeno himself probably did not believe in this world of contradictions, but he made these arguments as a sort of defense of Parmenides philosophy. This quote from Plato's dialogue Parmenides gives an explanation for why the Paradoxes of Zeno exist.
"The treatise is in truth a sort of support for Parmenides’ doctrine against those attempting to ridicule it on the ground that, if one is, the doctrine suffers many ridiculous consequences that contradict it. This treatise, therefore, argues against those who say the many are, and it pays them back with the same results and worse, intending to demonstrate that their hypothesis “if many are” suffers even more ridiculous consequences than the hypothesis of there being one, if one pursues the issue sufficiently."
Just for fun, I will try and explain away a few of the most famous of Zeno's paradoxes. Four of the ten known paradoxes are grouped as the paradoxes of motion. They seek to prove that movement is impossible because it creates contradictions. The most famous of these is called The Achilles. According the the paradox, a fast runner (Achilles) can never catch up to a slow runner (turtle) if the slow runner starts the race ahead. This is because by the time Achilles reaches the point where the turtle started, the turtle will have already moved on to another point ahead. By the time Achilles has reached the second point, the turtle has moved on to a third, and so on.
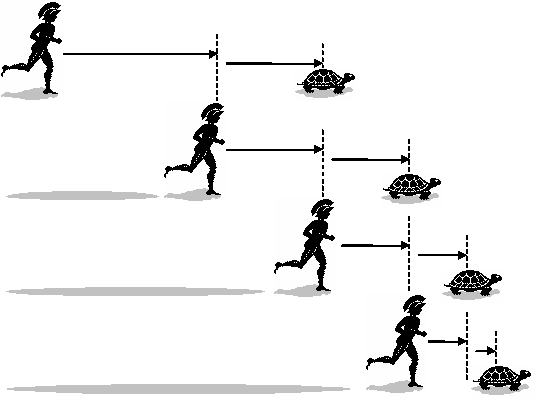
The problem here is one of dimensions. A point has 0 dimensions. A line has 1 dimension and one measurement, length. Because a line has a dimension that a point does not, a line can contain an infinite number of points. Likewise a 2 dimensional shape can contain an infinite number of 1 dimensional lines. So while Achilles has to cross an infinite number of potential points in order to reach the turtle further down the line, it does not take Achilles infinite time in order to do so, because Achilles is a flesh and blood person in a four dimensional universe and not a point on a page. In order to move in space, one must also move in time. This explains the contradiction without violating the view that the universe is one. The other paradoxes of motion can be explained away in similar ways or using math.
Then there are the paradoxes of plurality. These seek to directly prove that there cannot be multiple things because of contradictions. These are the ones that are explained by differentiating between language and reality. For example, the paradox of like and unlike is stated by Plato in Parmenides as being "If things are many, . . . they must be both like and unlike. But that is impossible; unlike things cannot be like, nor like things unlike." Likeness is not an ironclad law of the universe, it is a subjective relationship imposed upon the world by the mind.
The most interesting of the paradoxes of plurality, and of Zeno's paradoxes in general in my opinion, is that of Infinite Divisibility. Break down everything in the universe into it's component parts, until you reach the elements, which is amusingly the word that Zeno used to refer to whatever the quintessential substance is. I'll quote the Internet Encyclopedia of Philosophy because I'm lazy.
"Here there is a problem about reassembly. There are three possibilities. (1) The elements are nothing. In that case the original objects will be a composite of nothing, and so the whole object will be a mere appearance, which is absurd. (2) The elements are something, but they have zero size. So, the original object is composed of elements of zero size. Adding an infinity of zeros yields a zero sum, so the original object had no size, which is absurd. (3) The elements are something, but they do not have zero size. If so, these can be further divided, and the process of division was not complete after all, which contradicts our assumption that the process was already complete. In summary, there were three possibilities, but all three possibilities lead to absurdity. So, objects are not divisible into a plurality of parts."
(http://www.iep.utm.edu/zeno-par/#H3)
I think I have a partial answer for this one. Even if we assume the universe is finite, it can still contain an almost infinite number of "things" because of our ability to distinguish between "things" in different ways. In a more physical sense, we already know that physically splitting things into their component parts is not feasible in reality. If you cut an atom in half, you don't get two halves of an atom, you get an explosion. So even if there is a base particle that constructs the entire universe, we won't be able to divide our way to it. The Heisenberg Uncertainty Principle also plays into this.
I'll include The Millet Seed as a bonus paradox, because it makes Aristotle look like an idiot. If a bushel of grain falls to the ground, it makes a sound. Because it is composed of individual grains, each individual grain should make a sound if it falls. The same is true for 1/1000th of a grain. And yet we hear no sound when 1/1000 of a grain is dropped. Today we know this is just because our ears aren't sensitive enough to pick up the sound vibration, but according to Aristotle, Zeno was just wrong because parts do not necessarily have the properties of their whole. Aristotle stop, being able to make sound is not a property. Put on the dunce cap.