Own your network.
Launch an app in minutes for your brand on your website, iOS and Android. Build custom integrations.
Access millions of people across decentralized social media.
Build your community. Don't rely on big tech.
Quickly launch your own social media app, on the web and in the app stores. Build a new community or onboard one you've already got, empowering people to communicate, share, and grow. Available now with custom domains on web, Android and iOS. Interoperable with web2 and web3 protocols like ActivityPub, RSS, DNS, Bitcoin, Ethereum, Stripe and more.
Grow your audience. Sell memberships for exclusive access. Monetize with ads. Notify your audience. Add comments to your website."
Own the code. Data. Contacts. Content. Communications. Create public and private communities.
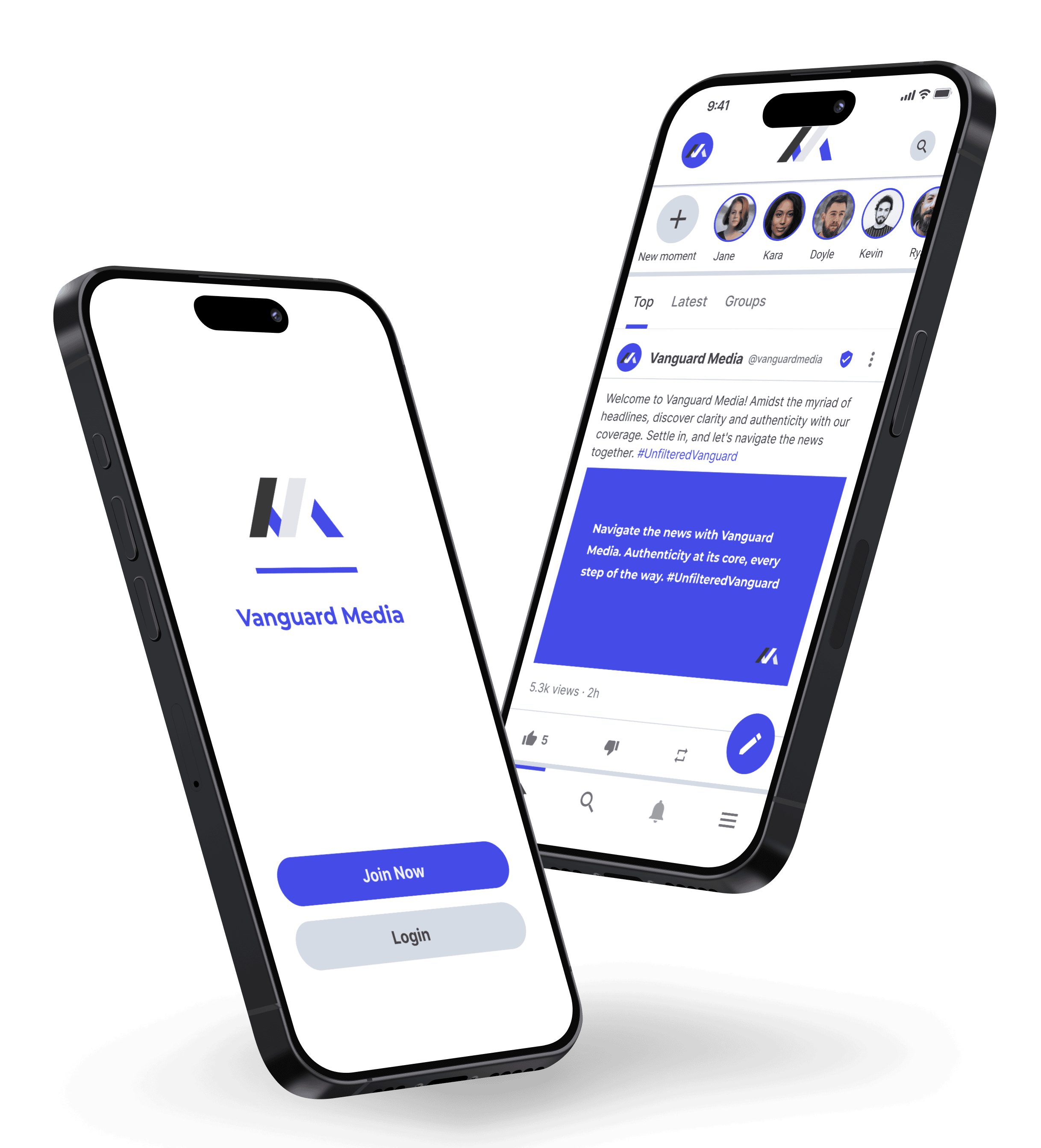
Join millions on Minds
Minds.com is the one of the largest networks in the decentralized social media space and has generated more than a billion views. We believe freedom of speech and open dialogue are the solution to these polarized times.
If you aren't ready to launch your own app, join our active community to connect with people, speak your mind and reach new audiences. Connect with top creators, independent journalists and artists.
Features include Newsfeed. Explore. Search. Groups. Chat. Blogs. Video. Photos. Tips. Memberships. Paid Replies. Notifications. Chat. Boost. Affiliate. Rewards. Analytics. Monetization. Rewards.
